[CodeKata] 프로그래머스 : 3.18(목), 배달 / [이론] Dijkstra Algorithm

🥋 Ooooth!! (Level 2) : 배달

 

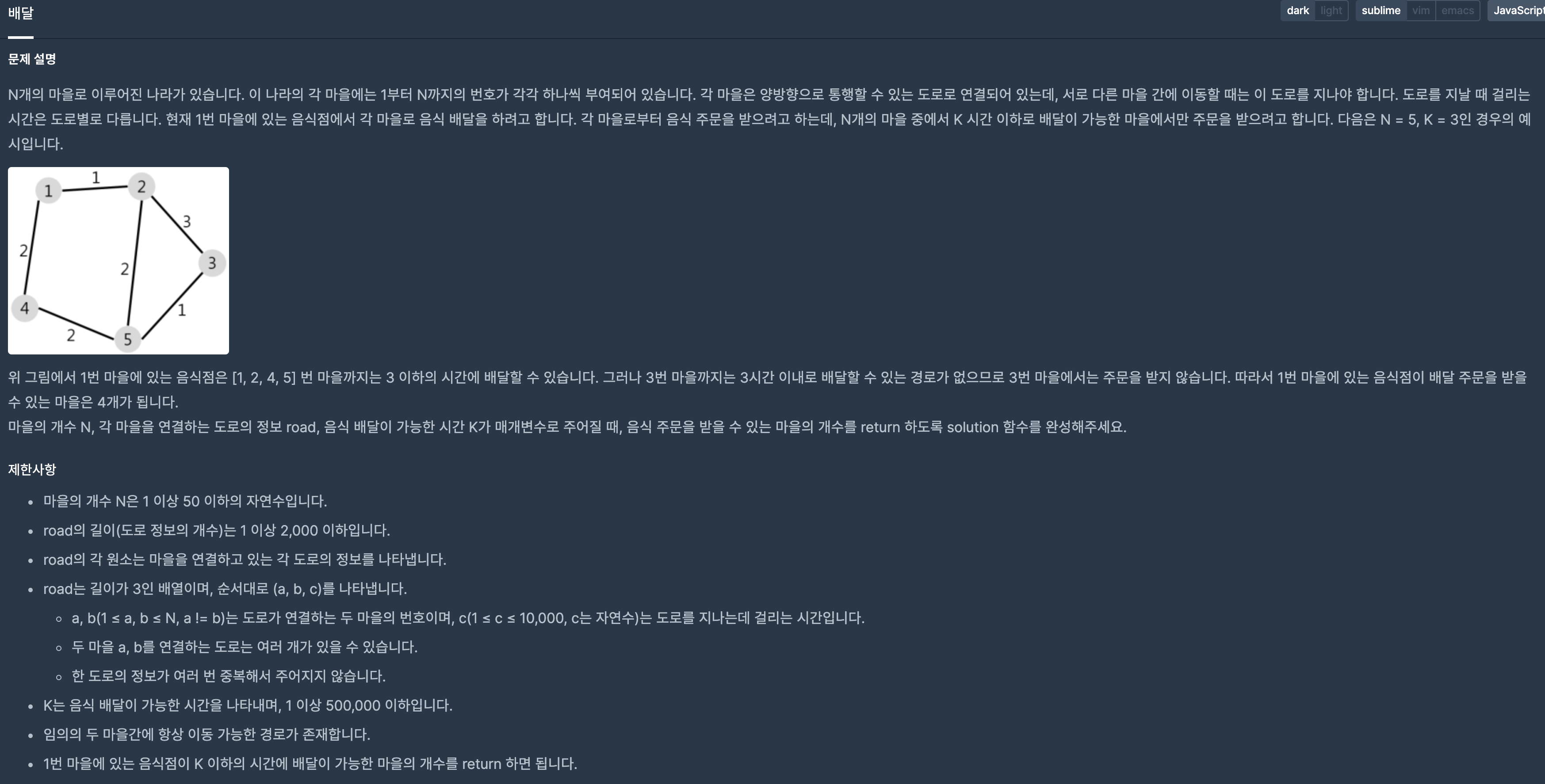
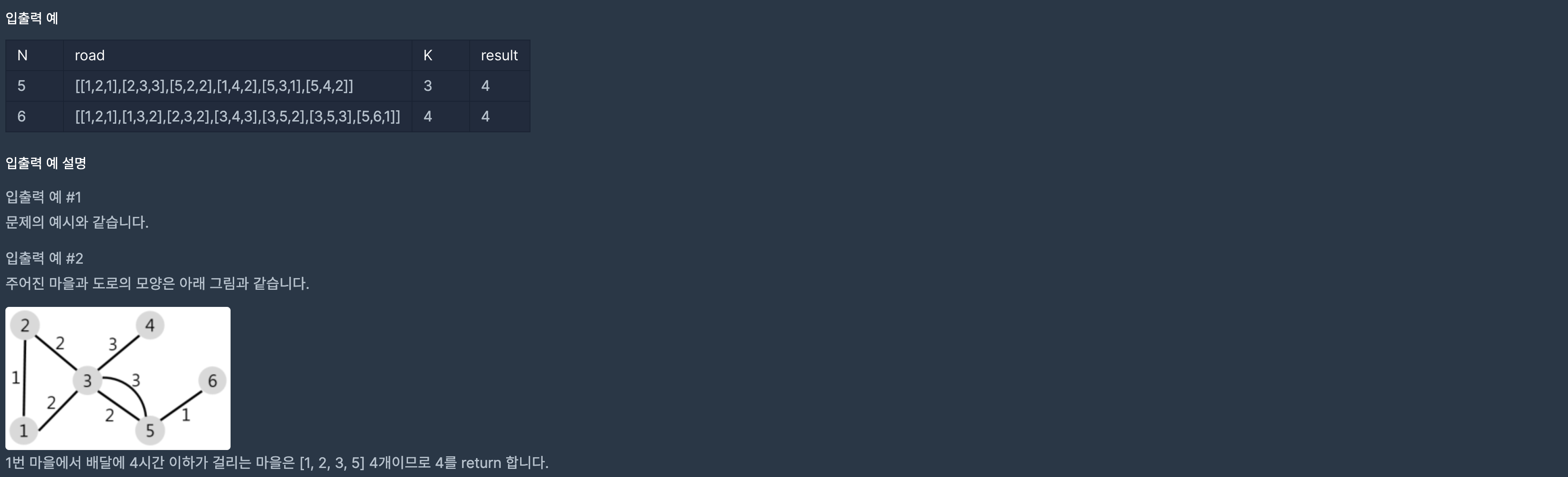
🧮 풀이

다익스트라 알고리즘을 사용해 최단시간을 탐색하는 문제였다. 리뷰에서, 다익스트라에 대해 자세히 정리했다.

function solution(N, road, K) {
  let arr = Array(N + 1).fill(Infinity);
  let adj = Array.from(Array(N + 1), () => Array());

  road.forEach(info => {
    let a = info[0];
    let b = info[1];
    let c = info[2];

    adj[a].push({ to: b, weight: c });
    adj[b].push({ to: a, weight: c });
  });

  let check = [{ to: 1, weight: 0 }];
  arr[1] = 0;
  while (check.length) {
    let edge = check.pop();
    adj[edge.to].forEach(next => {
      if (arr[next.to] > arr[edge.to] + next.weight) {
        arr[next.to] = arr[edge.to] + next.weight;
        check.push(next);
      }
    });
    check.sort((a, b) => b.weight - a.weight);
  }
  return arr.filter(time => time <= K).length
}

1. arr는 각 인덱스(노드)까지의 최단거리를 저장한다.(최초는 Infinity) adj는 노드간의 경로정보를 저장하는 배열이다.
2. road 배열을 순회하며 adj 배열에 경로정보를 저장한다. 인덱스(a)에, 갈 수 있는 노드(b)와 소요시간(c)를 객체형태로 담았다.
3. 출발점이 1번 노드이므로, check 스택에 이를 담아준다. 1번노드의 최단거리는 0이므로, arr[1]은 0이다.
4. while 반복문을 check 스택이 빌 때까지 순회한다. edge는 스택 맨 뒤에서 뽑은 경로 이동정보이다.
5. edge.to는 출발노드이므로, adj[edge.to]는 갈 수 있는 인접노드들의 배열이 될 것이다. 이를 순회하며, 인접노드의 arr 경로값과 현재노드 경로값 + 인접노드 소요시간 중 작은 값을 arr에 최신화한다. 이후, 이를 다시 check 스택에 담아준다.
6. arr에는 1번 노드에서 각 노드까지 최단시간이 저장되어있다. 이를, K 이하인 값들로 필터링한 뒤 길이값을 반환한다.

 

🖇 리뷰

- 다익스트라 알고리즘(Dijkstra Algorithm)

 

네덜란드의 컴퓨터 과학자 에츠허르 다익스트라가 고안한 길찾기 알고리즘이다. 노드 사이 간선(Edge)에 양의 가중치를 갖는 그래프에서 최단경로를 찾을 때 사용할 수 있다.

 

통상, 최단경로 탐색에서는 BFS(너비우선 탐색)을 주로 사용한다. 이는, 간선들의 연결여부(1 or 0) 조건을 기반으로 탐색한다.

다익스트라는 간선의 연결뿐만 아니라 가중치까지 고려한 최단경로 탐색이 가능하다. 즉, 가중치 = 소요시간으로 생각하면 최단시간 경로가 나오는 것이다.

 

* 다익스트라 탐색 과정

 

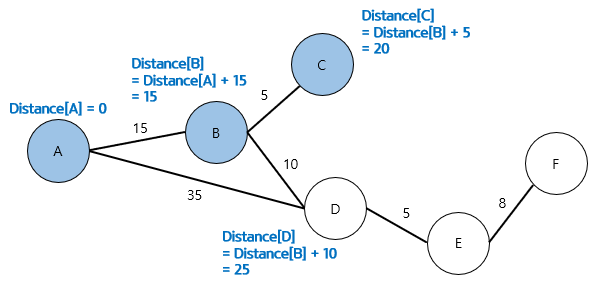
1) 출발지를 선택하고 Distance를 0으로 설정한다. 

2) 출발지와 연결된 노드의 Distance를 업데이트한다.

3) 현재까지 업데이트된 Distance를 보고 가장 좋은 길(즉, 최단 거리의 길)을 선택한다. (여기선 B)

4) 현재까지 업데이트된 Distance와 이전 단계에서 선택된 노드의 Distance를 업데이트한다. 
   이때, 이미 Distance가 업데이트된 노드라도 더 짧은 경로가 있다면 업데이트 해주어야한다

원래 D의 Distance는 A에서 직행하는 경로로 35였지만 B를 경유하는 경로인 25가 더 가깝기 때문에 Distance를 Update

5) 현재까지 업데이트된 Distance를 보고 가장 좋은 길(즉, 최단 거리의 길)을 선택한다. (이번엔 C)

6) 이전 단계에서 선택된 노드와 연결된 노드가 없다면 선택된 노드 다음으로 짧은 거리인 노드를 선택한다. (D로 넘어감)

7) 이전 단계에서 선택된 노드와 연결된 노드의 최단 거리를 업데이트해준다.

8) 선택되지 않은 노드 중 Distance가 가장 짧은 것을 선택한다. (여기선 E)

9) 이전 단계에서 선택된 노드와 연결된 노드의 최단 거리를 업데이트해준다.

10) 선택되지 않은 노드 중 Distance가 가장 짧은 것을 선택한다. (마지막 F)

11) 모든 노드를 확정했다면 탐색을 종료한다.

 

 

* BFS(너비우선 탐색) 탐색 과정 비교

 

그래프를 탐색할 떄, 같은 깊이에 해당하는 노드부터 탐색하고 더 탐색할 수 없으면 다음 깊이를 탐색하는 알고리즘이다.

1) A와 연결된 노드는 B와 C 입니다. A는 자신과 연결된 2개의 노드 중 어떤 노드를 선택할 지 고릅니다.
   저는 노드를 선택해야 할 경우, 그림에서 보았을 때 가장 위쪽에 선택하는 노드를 고르도록 하겠습니다.
  ▶ 선택된 노드는 "B"입니다.

2) B와 같은 깊이에 해당하는 노드는 C입니다.
  ▶ 선택된 노드는 "C"입니다.

3) C와 같은 깊이에 해당하는 노드 중 탐색하지 않은 노드가 없습니다.
   더 깊은 곳을 탐색합니다.

4) 다음 깊이에 해당하는 노드는 D, E, F 입니다.
   제일 위쪽 노드인 D부터 탐색하겠습니다.
  ▶ 선택된 노드는 "D"입니다.

 

5) D와 같은 깊이에 해당하는 노드는 E, F 입니다.
   저는 위쪽 노드인 E부터 탐색하겠습니다.
  ▶ 선택된 노드는 "E"입니다.

 

6) 남은 노드인 F를 선택합니다.
  ▶ 선택된 노드는 "F"입니다.

 

7) F와 같은 깊이에 해당하는 노드 중 탐색하지 않은 노드가 없습니다.
   더 깊은 곳을 탐색합니다.

 

8) 다음 깊이에 해당하는 노드는 G 입니다.
  ▶ 선택된 노드는 "G"입니다.

 

 

이전에 파이썬 알고리즘을 공부할때도, 다익스트라 알고리즘은 접해보지 못해 새롭게 알게된 개념이다.

물론, "양의 가중치" 라는 한정적인 상황에서 적용하지만, 이 가중치가 이번 문제에서의 시간처럼 다양한 응용형태로 나올 수 있겠다고 느꼈다.