[CodeKata] 위클리 프로그래머스(2월 3주차)

Algorithm

[CodeKata] 위클리 프로그래머스(2월 3주차)

ttaeng_99 2021. 2. 15. 15:22

🥋 Ooooth!! (Level 2)

코드카타에 들이는 시간이 많아졌지만, 그만큼 풀었을 때 쾌감도 정말 짜릿하다!

당분간 3차 프로젝트를 위한 공부의 기간이기 떄문에, 바이오리듬 유지하면서 오전에 알고리즘에 몰두하도록 해야겠다.

👊 2.15(월) / 멀쩡한 사각형

📜 문제

🧮 풀이

풀이를 설계하는 과정을 먼저 설명해야 코드풀이가 가능할 것 같다.

위 예시는, 8 * 12 박스의 대각선 경우이다. 대각선은 2 * 3 박스를 기준으로 총 4회 반복되었다.

이 4의 의미를 고민했고, 이것이 너비(8)와 높이(12)의 최대공약수 임을 확인했다. (다른 경우로, 5 * 3 이라면 1이 되야겠다.)

대각선 최소단위(너비, 높이를 최대공약수로 나눈)에서 빠진 박스 개수를, 최대공약수 만큼 곱해주면 전체 빠진 박스개수가 나온다.

이를 전체 개수에서 빼줘서 정답을 도출하는 것으로 생각하고 문제를 풀었다.

function getGCD(a,b) {
  let min = Math.min(a,b)
  let max = Math.max(a,b)
  let r = max % min
  return r === 0 ? min : getGCD(min, r)
}

function solution(w, h) {
  const gcd = getGCD(w,h)  
  const diagW = w/gcd;
  const diagH = h/gcd;
  const diagUnit = diagW*diagH - ((diagW - 1) * (diagH - 1));
  const diagTotal = diagUnit * gcd
  return w * h - diagTotal
}

최대공약수를 구하는 getGCD() 함수를 만들었다. 유클리드 호제법을 기반으로 한 재귀함수이다.
gcd 변수에 최대공약수를 담는다. 대각선 단위의 너비(diagW), 높이(diagH)는 본래 너비, 높이를 gcd로 나눈 값이다.
대각선 단위에서 남은 박스개수는 diagW와 diagH에서 1씩 뺀 값을 곱한 사각형이 된다.
반대로, 빠진 박스개수는 대각선 단위 전체개수(diagW * diagH)에서 위 값((diagW - 1) * (diagH - 1))을 빼준다.
전체 빠진 박스개수(diagTotal)는, 대각선 단위 빠진 박스개수(diagUnit)와 gcd 의 곱이 된다.
이를 , 전체 개수인 w * h에서 빼면 총 남은 박스개수가 된다. 해당값을 반환하면 된다.

🖇 리뷰

- 유클리드 호제법

두 수의 최대공약수를 구하는 방법은 2가지가 있다.

1) 두 수를 각각 나눴을 때 나머지가 0인 수 중에 가장 큰 수가 최대공약수이다. 이를, 반복문으로 구한다. (범위는, 둘 중 작은수 이하)

let gcd = 0;
let num = [a, b];

for(let j = Math.min.apply(null, num) ; j >= 1 ; j--) { 
  if ((Math.min.apply(null, num)%j == 0) && (Math.max.apply(null, num)%j == 0)) { 
    gcd = j;
    break;
  } 
}

2) 유클리드 호제법으로 구한다. a % b = r 이라고 했을 때, (a, b)의 최대공약수는 (b, r)의 최대공약수와 같다는 원리이다. (a > b)

이를, b % r = r' 로 다시 나눠서, 나머지가 0이 될 때까지 반복한다. 0이 된다면, 둘 중 작은값(b 혹은 r) 이 둘의 최대공약수가 된다.

function gcdlcm(a, b) {
    var answer = [];
    var minNum = Math.min(a, b);
    var maxNum = Math.max(a, b);
    answer[0] = gcd(minNum, maxNum);
    answer[1] = lcm(minNum, maxNum);
    return answer;
}

// 최대공약수
function gcd(minNum, maxNum){
  return (maxNum % minNum) === 0 ? minNum : gcd(minNum, maxNum % minNum);
}

// 최소공배수
function lcm(minNum, maxNum){
  return minNum * maxNum / gcd(minNum, maxNum);
}

이처럼, 나머지가 0이면 minNum을, 아니라면 gcd() 함수를 재실행하는, gcd() 재귀함수를 활용하면 된다.

최소공배수는, minNum 과 maxNum 의 곱에서 최대공약수를 나눠주면 된다.

* 출처: swess 님의 블로그 (swess.tistory.com/13)

- 모범예시

// 유클리드 호제법을 이용한 최대 공약수 구하기
function gcd(w, h) {    // 처음 W와 H를 받습니다.

    // W와 H의 나머지를 구합니다.
    const mod = w % h;
    // 만약 나머지가 0일 경우 H를 반환합니다.
    if (mod === 0) {
        return h;
    }
    // 만약 0이 아닐경우 W에 H를 넣고 H에 나머지인 mod를 넣어 해당 함수를 다시 호출해 줍니다.
    return gcd(h, mod);
}

function solution(w, h) {
    // 최대 공약수를 구해줍니다.
    const gcdVal = gcd(w, h);
    // 공식에 맞춰 사용
    return w * h - (w + h - gcdVal);
}

* 출처: noogoonaa.tistory.com/74

전체 개수(w * h)에서, (w + h - gcd)를 빼면 된다고 하는데.... 사실 공식 자체가 이해가 되진 않았다. (이해가 되신분은 댓글을...😅)

아마, 대각선이 꺾이는 부분에서 너비와 높이가 한 칸씩 겹치기 때문에 이를 빼준다는 개념인 것 같다.

내 풀이는 코드도 길고 그만큼 계산량도 많지만, 반복적인 패턴에 대해서 이해하기엔 용이한 방법인 것 같다.

👊 2.16(화) / 문자열 압축

📜 문제

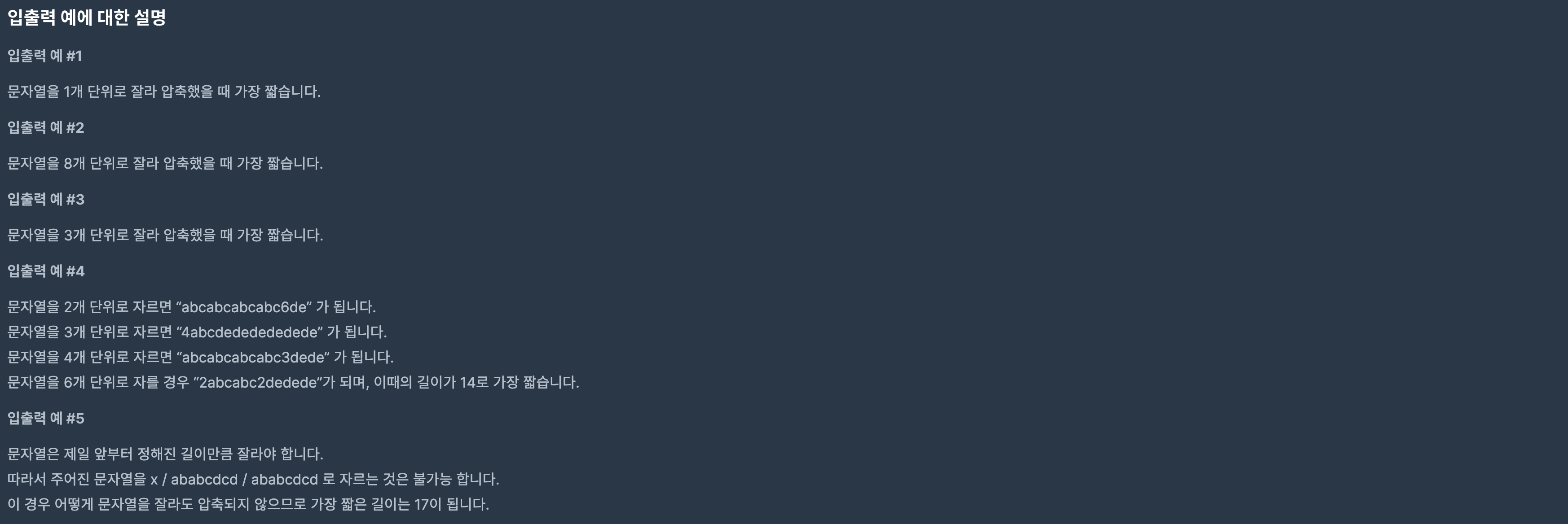
요약하면, 문자열(s)를 1부터 전체 길이값까지 반복해서 잘라가면서, 겹치는 문자가 있으면 앞에 숫자를 더한다.

이렇게 수정한 문자열의 길이들 중, 가장 짧은 케이스의 길이값이 결과가 되는 것이다.

🧮 풀이

function solution(s) {
  let minLen = 1000;
  for (let l = 1 ; l <= s.length ; l++) {
    let strArr = [];
    let i = 0
    while (i < s.length) {
      const strUnit = s.substr(i, l);
      const lastIdx = strArr.length - 1;
      if (strArr[lastIdx] === strUnit) {
        if (typeof strArr[lastIdx-1] === 'number') {
          strArr[lastIdx-1]++
        }
        else {
          strArr.splice(lastIdx, 0, 2)
        }
      }
      else {
        strArr.push(strUnit)
      }
      i += l
    }
    const strLen = strArr.join('').length
    minLen = strLen < minLen ? strLen : minLen;
  }
  return minLen
}

최소값(결과)이 될 minLen 변수를 선언한다. 문자열이 최대 1000자이므로, 비교연산을 위해 1000이라는 값을 주었다.
2중 반복문을 활용한다. l은 문자열을 자를 단위길이가 된다. 범위는, 1부터 문자열(s)의 길이까지이다.
자른 문자들을 담는 strArr 배열을 선언한다. 자르기가 완료되면, join으로 합친 문자열 길이(strLen)를 최소값과 비교한다.
i는 문자열을 자르기 시작하는 인덱스이다. while 반복문 내 조건처리가 끝나면, 단위길이(l)만큼 계속 더해준다.
첫 번째 조건은, strArr 끝값과 현재 자른 문자열(strUnit)과 같은지다. 같다면 두 번째 조건, 다르면 push를 한다.
두 번째 조건은, 숫자를 세는 것이다. 이미, 같은 문자열 앞에 숫자가 있다면 + 1, 없다면 문자열 앞에 2를 넣는다.(splice)

🖇 리뷰

const solution = s => {
  if (s.length === 1) return 1;
  let length = s.length;
  let prevValue = "";
  let cnt = 0;
  let result = [];
  for (let i = 1; i <= length / 2; i += 1) {
    let compArray = [];
    prevValue = s.substring(0, i);
    cnt = 1;
    compArray[0] = prevValue;
    for (let j = i, c = 0; j < length; j += i) {
      let nowValue = s.substring(j, j + i);
      if (nowValue === prevValue) {
        compArray[c] = ++cnt + nowValue;
      } else {
        cnt = 1;
        compArray[++c] = nowValue;
      }
      prevValue = nowValue;
    }
    result[i - 1] = compArray.reduce((total, cur) => (total += cur.length), 0);
  }
  return result.sort((a, b) => a - b)[0];
};

풀이이해가 쉽진 않지만, 풀이 포인트의 좋은점이 몇 가지 있어 가져와봤다.

s.length가 1인 경우, 1을 그대로 반환했다. 좋은 예외처리이다.
또한, 문자열을 자르는 단위는 전체길이(s.length)의 절반까지만 한다. 이것이 넘어가면, s.length가 최소길이가 되기 때문이다.

👊 2.17(수) / 삼각 달팽이

📜 문제

🧮 풀이

function solution(n) {
  const ansArr = Array.from(new Array(n), () => []);

  let l = n;
  let num = 1;
  let i = 1;
  while (l > 0) {
    const lastIdx = n - i;
    for (let a = 0 ; a < l ; a++) {
      ansArr[2*(i-1) + a].splice(i-1, 0, num)
      num++
    }
    for (let b = 0 ; b < l-1 ; b++) {
      ansArr[lastIdx].splice(b+i, 0, num)
      num++
    }
    for (let c = 0 ; c < l-2 ; c++) {
      ansArr[lastIdx-c-1].splice(ansArr[lastIdx-c-1].length+1-i, 0, num)
      num++
    }
    l -= 3;
    i += 1;
  }
  return ansArr.reduce((acc, cur) => acc.concat(cur))
}

삼각 달팽이를 말 그대로 코드로 옮겨놓은 풀이다. 먼저, 피라미드를 쌓을 2차원 배열(ansArr)을 만든다.
l은 변의 길이이다. n = 6 인 경우, 달팽이는 바깥기준 왼쪽 6, 아래 5, 오른쪽 4개의 숫자를 두른다.
그 다음, 안쪽 변은 왼쪽 3, 아래 2, 오른쪽 1개의 숫자를 두른다. 그렇기 때문에, 반복마다 l을 3씩 빼준다.
num은 우리가 넣을 숫자이다. 매번 숫자를 두를 때마다, num++로 숫자값을 증가시켜준다.
i는 두르는 횟수라고 생각하자. 이 두르는 횟수는 각 변의 시작점이나 splice 인덱스를 잡는데 유용하다.
왼쪽(a)/시작점: [2*(i-1)] 부터이다. 첫 번째는 0번줄, 두 번째는 2번줄, 세 번째는 4번줄의 규칙성을 보이기 때문
왼쪽(a)/splice: 인덱스는 i-1이다. 첫 번째는 0번째, 두 번째는 1번째, 세 번째는 2번째 삽입 규칙성을 가짐
아래(b)/위치: lastIdx 이다. 이 lastIdx는 n-i 로, 맨 밑에서부터 한 칸씩 올라오는 값을 가짐
아래(b)/splice: 인덱스는 b+i이다. 첫 번째는 1번째 부터 5개, 두 번째는 2번째부터 2개 의 규칙성을 보이기 때문
오른쪽(c)/시작점: [lastIdx-1] 부터이다. 아래를 다 채웠으니, 그 바로 위부터 시작하기 위해 -1을 해준다.
오른쪽(c)/splice: 해당원소(ansArr[lastIdx-1-c]의 길이값에서 i씩 빼주면서 splice 인덱스를 잡아야 한다.

설명이 길고 어렵지만, 삼각 달팽이를 직접 그려보면서 규칙성을 그대로 구현한다 생각하면 단순한 작업이다.

안의 숫자값들을 처음엔 배열로 만들어서 넣어줬다. (Array.from(), 전체 길이는 n(n+1)/2, splice 시 num 대신 shift() 값)

위처럼 풀었더니, 배열을 생성하고 shift() 하는데 있어 시간초과가 발생했다. 그래서, 이처럼 숫자누적으로 변경한 것이다.

🖇 리뷰

아~~~~~주 좋고 직관적인 풀이가 있어 가져왔다.

처음 answer 배열을, 미리 빈 값을 가진 달팽이로 만든다. 이를 통해, answer[x][y] 좌표값에 접근하면서 값을 넣을 수 있는 것이다.

function solution(n) {
    const answer = new Array(n).fill().map((_, i) => new Array(i + 1));
    
    let count = 0;
    let x = -1;
    let y = 0;
    while (n > 0) {
        for (let i = 0; i < n; i++) answer[++x][y] = ++count;
        for (let i = 0; i < n - 1; i++) answer[x][++y] = ++count;
        for (let i = 0; i < n - 2; i++) answer[--x][--y] = ++count;
        n -= 3;
    }
    
    return answer.flatMap(e => e);
}

빈칸으로 이루어진 2차원 배열(answer)를 만들었다. 행은 Array(n), 열은 Array(i+1) 만큼 만들어준 것이다.
while 안의 세 개의 for문은 각각의 변을 의미한다. 또한, answer[x][y]로 2차원 배열 좌표에 숫자값(count)을 넣으면서 더해준다.
flatMap() 메서드는 2차원 배열을 1차원 배열로 가공해주는 메서드이다.

👊 2.18(목) / 큰 수 만들기

📜 문제

🧮 풀이

function solution(number, k) {
  while (k > 0) {
    let newNum = 0;
    for (let i = 0 ; i < number.length ; i++) {
      const cutNum = Number(number.slice(0,i) + number.slice(i+1));
      if (cutNum > newNum) {
        newNum = cutNum
      }
    }
    number = newNum.toString();
    k--;
  }
  return number;
}

이처럼, k번 반복하면서 한글자씩 자른 숫자의 최대값을 최신화하는 로직을 짰다.

하지만, 실패 및 시간초과가 75% 발생하여서 좀 더 좋은 풀이를 찾아보았다.

🖇 리뷰

stack 을 이용한 풀이인데, 최대한 이해를 해보려고 노력했다.

function solution(number, k) {
    let stack = [];
    for (let i = 0; i < number.length; i++) { 
        const now = number[i];         
        while (k > 0 && stack[stack.length - 1] < now) {
            stack.pop();
            k--;
        }
        stack.push(now);
    }
    stack.splice(stack.length - k, k);
    const answer = stack.join('');

    return answer;
}

먼저, 정답 숫자들이 쌓일 stack 배열을 만들어준다.
number 숫자들을 순회하면서 스택을 쌓아간다. 처음은, 바로 push가 된다.
두 번째 부터는, 현재값이 stack 끝값보다 크다면 stack 끝값을 pop() 한 뒤 현재값을 넣고 k를 감소시킨다.
만약, number 자체가 정답이면 pop() 이 일어나지 않을 것이다. 예) solution('1010', 2) => '1010'
이 때, k 역시 소모되지 않고 남아있으므로(2), 남은 k만큼 뒷 부분을 잘라줘야 우리가 원하는 길이만큼 남는다.

👊 2.18(목) / 조이스틱

📜 문제

🧮 풀이

function changeChar(l) {
  const charL = l.charCodeAt();
  return  charL < 78 ? charL - 65 : 91  - charL
}

function solution(name) {
  let nameArr = name.split('').map(l => changeChar(l));
  let stickIdx = 0;
  let stickDir = (nameArr[nameArr.length-1] !==0 && nameArr[nameArr.length-1] < nameArr[1]) || nameArr[1] === 0 ? -1 : 1;
  let answer = 0;
  answer += nameArr[stickIdx];
  nameArr[stickIdx] = 0;
  while (nameArr.reduce((acc, cur) => acc + cur) !== 0) {
    answer++;
    stickIdx = stickIdx + stickDir < 0 ? nameArr.length - 1 : stickIdx + stickDir;
    answer += nameArr[stickIdx];
    nameArr[stickIdx] = 0;
  }
  return answer
}

🖇 리뷰

위처럼 풀었을 때, 테스트 케이스 11만 실패가 발생한다. 이유는, 한쪽으로만 가지 않는 경우때문 ('BABAAAB')

findIndex() 메서드로 0이 아닌 값들의 위치를 찾아, 현재 인덱스와 거리를 비교했지만 런타임 에러가 발생했다.

function solution(name) {
    let sum = 0;
    for (let i = 0; i < name.length; i++) {
        let diff = name[i].charCodeAt() - 'A'.charCodeAt();
        sum += diff > 13 ? 26 - diff : diff;
    }

    let minMove = name.length - 1;
    for (let i = 1; i < name.length; i++) {
        if (name[i] === 'A') {
            for (var j = i + 1; j < name.length; j++) {
                if (name[j] !== 'A') {
                    break;
                }
            }

            const left = i - 1;
            const right = name.length - j;
            minMove = Math.min(minMove, left > right ? left + right * 2 : left * 2 + right);

            i = j;
        }
    }

    return sum + minMove;
}

2단계인데도 이렇게 어렵다니... 1단계에 자만한 내가 부끄러워졌다.

문제를 구현하는 로직도 로직이지만, 오늘 문제처럼 예외처리에 대한 고민이 많아진다.